 جدید
جدیدتنش و کرنش به زبان ساده
مقدمه
منحنی تنش کرنش یکی از اولین منحنیها یا نمودارهای استحکام مواد است که مهندسین بسیاری از جمله مواد و مکانیک هنگام آغاز یادگیری علم مواد به آن مواجه میشوند. بطور کلی مفاهیم مکانیکی تنش و کرنش، ثمره اثراتی هستند که یک قطعه از نیروهای داخلی و خارجی دریافت میکند.
ممکن است مشاهده این نمودار و مفاهیم مربوط به آن در ابتدا دلهرهآور و سخت به نظر برسد اما در واقع اینطور نیست. ما در این مقاله کوشش کردهایم به زبان ساده مفاهیم مرتبط با تنش و کرنش را به شما آموزش دهیم به نحوی که با مطالعه آن، این مفاهیم در ذهن شما تثبیت شوند. پس تا پایان مقاله همراه ما باشید.
تنش (Stress) چیست؟
طبق یک تعریف کلی و ساده، تنش به عنوان نیرویی در واحد سطح تعریف میشود که در انواع مختلف مواد هنگام اعمال نیروی خارجی مشاهده میشود.
جهت تجزیهوتحلیل مفهوم تنش و کرنش، فرض تعادل قطعه جهت بهکار گرفتن معادلات استاتیکی اولین اقدامی است که باید در نظر گرفته شود.
با توجه به نکتهای که مطرح شد، در ذهن خود یک قطعه با سطح مقطع A تصور کنید که نیروی کششی خارجی P به آن اعمال شده است. درمقابل نیروی P، یک نیروی داخلی برابر با انتگرال تنش در دیفرانسیل سطحی (dAσ∫)، با نیروی خارجی وارد شده مقاومت میکند. در اینجا σ، تنش محوری یا عمود به صفحه است. با فرض یکنواختبودن تاثیر تنش روی سطح مقطع، معادله 1 بهدست میآید.
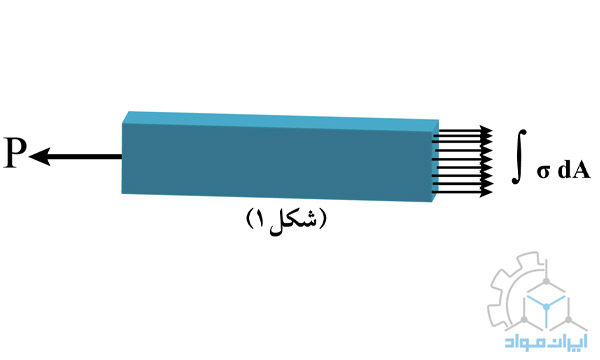
معادله1:
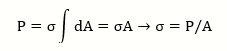
واحد تنش چیست؟
واحد تنش در سیستم بینالمللی SI، نیوتون بر متر مربع (N/m2) است که به نام پاسگال (Pa) معروف است.
کرنش (strain) چیست؟
برای پیبردن به مفهوم کرنش، یک میلهی استوانهای یکنواخت را در نظر بگیرید که تحت بار کششی محوری P قرار میگیرد.
فرض کنید که دو علامت روی سطح میله در حالت بدون کشش قرار میگیرند و L0 طول بین این دو علامت است. یک نیرو P به یک انتهای میله اعمال میشود و میله افزایش طول و کاهش قطر را تجربه میکند. فاصله بین علائم به میزان δ افزایش مییابد که «تغییر شکل» نامیده میشود.
کرنش خطی متوسط مهندسی، نسبت تغییر طول به طول اولیه است که با e نشان داده میشود (معادله2).
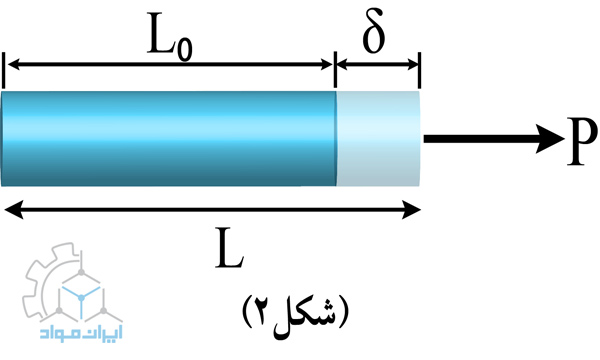
معادله 2:
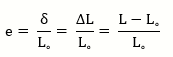
واحد کرنش چیست؟
کرنش یک مقدار بدن واحد است چون واحدهای صورت و مخرج یکی هستند.
فرضیات مهم در تعریف تنش و کرنش
پس از تعریف دو مفهوم مهم تنش و کرنش نیاز است به چند نکته اشاره شود:
مفروضات مهم در استحکام مواد این است که جسم مورد تجزیه و تحلیل پیوسته (Continuous)، همگن (Homogeneous) و همسانگرد (Isotropic) است.
جسم پیوسته: جسمی است که فاقد هر نوع حفره یا فضای خالی باشد.
جسم همگن: جسمی همگن است که در تمام نقاط دارای خواص یکسان باشد.
جسم همسانگرد: زمانیکه یک ویژگی با جهت تغییر نکند، جسم نسبت به آن خاصیت همسانگرد در نظر گرفته میشود. خاصیتی که با جهتگیری با توجه به سیستم محورها تغییر میکند، ناهمسانگرد است.
عواملی که باعث توزیع غیریکنواخت تنش میشوند
معمولا بهدلیل عدمتوزیع یکنواخت تنش بهدلایل عنوانشده (عدم پیوستگی، ناهمگنی و ناهمسانگردی)، تنش متوسط بهجای تنش یکنواخت در معادله یک ارائه میشود. برای اینکه تنش کاملا بهصورت یکنواخت توزیع شود، هر عنصر طولی در میله باید دقیقا کرنش یکسانی را تجربه کنند و تناسب بین تنش و کرنش باید برای هر عنصر یکسان باشد. ناهمسانگردی ذاتی بین دانهها در یک فلز چند بلوره (Polycrystal)، امکان یکنواختی کامل تنش را روی بدنهای با اندازه ماکروسکوپی رد میکند.
وجود بیش از یک فاز نیز باعث عدمیکنواختی تنش در مقیاس میکروسکوپی میشود. اگر میله مستقیم نباشد یا بار مرکزی نداشته باشد، کرنشها برای برخی از عناصر طولی متفاوت بوده و تنش یکنواخت نخواهد بود. هنگامیکه فلزات بهشدت در یک جهت خاص تغییر شکل میدهند، مانند نورد یا آهنگری، خواص مکانیکی ممکن است در مقیاس ماکروسکوپی ناهمسانگرد باشد. نمونههای دیگر از خواص ناهمسانگرد مواد کامپوزیتی تقویتشده با الیاف هستند. اختلال شدید در یکنواختی الگوی تنش، زمانی رخ میدهد که تغییر ناگهانی در مقطع وجود داشته باشد؛ این مورد منجربه افزایش تنش یا تمرکز تنش میشود. تنش به دو صورت عمودی و برشی به سطح مقطع اعمال میشود.
چه تنشهایی به هر صفحه اعمال میشود؟
تنشها انواع مختلفی دارد که در ادامه بهبیان انواع آن میپردازیم:
تنش عمودی یا محوری (Axial Stress)
این تنش در امتداد عمود به سطح مقطع اعمال میگردد و به دو نوع زیر تقسیمبندی میشود.
تنش عمودی بزرگتر از صفر: تنش کششی
تنش عمودی کوچکتر از صفر: تنش فشاری
تنش برشی (Shear stress)
این تنش در صفحهی موردنظر یا سطح مقطع اعمال میگردد و با τ نمایش داده میشود.
تنشها در یک نقطه بهصورت مولفههای عمودی و برشی وجود دارند. xxσ یا xσ تنش عمودی در صفحه x و در راستای x است.
برای نمایش تنشهای برشی معمولا از دو اندیس استفاده میشود. اندیس اول صفحهای را مشخص میکند که تنش روی آن اعمال میشود و اندیس دوم جهت اعمال تنش را مشخص مینماید. بهعنوانمثال، τxy تنش برشی روی صفحه عمود بر محور x و در جهت y است. یک تنش برشی وقتی مثبت است که در جهت مثبت روی صفحه مثبت مکعب واحد اعمال شود و یا در جهت منفی روی صفحه منفی مکعب اعمال شود.
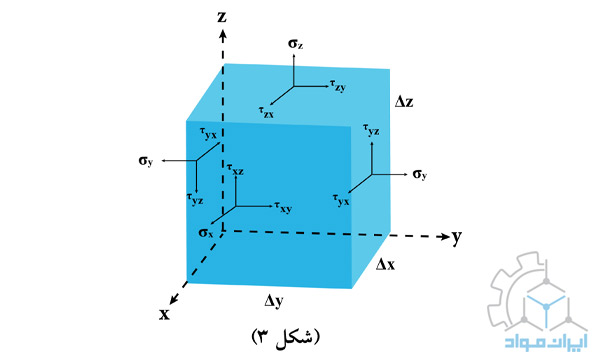
با توجه به شکل 3 و توضیحات قبل، با وجود سه تنش در هر صفحه مکعب جمعا 18 مولفه تنش در هر نقطه اعمال میشود. اما چون صفحات دوبهدو متناظر هستند بنابراین سه صفحه از آنها در نظر گرفته میشود و در مجموع نُه مولفه برای تعیین وضعیت تنش در یک نقطه نیاز است که عبارتنداز: xσ، yσ، zσ، xyτ، xzτ، yxτ، yzτ، zxτ، zyτ.
اگر فرض شود که مساحت سطوح مکعب به اندازهای کوچک باشد که تغییر تنش روی آن صفحات ناچیز باشد با محاسبه لنگر حاصل از نیروهای اعمالی نسبت به محور z مشاهده میشود:
معادله 3 | (τxy ΔyΔz)Δx = (τyx ΔxΔz)Δy →→ τxy = τyx |
و با محاسبه لنگر نسبت به محورهای x و y، معادلات زیر حاصل میشود.
معادله 4 | τyz = τzy |
معادله 5 | τzx = τxz |
بنابراین بهطورکلی حالت تنش با سه مولفهی عمودی xσ، yσ، zσ و سه مولفهی برشیxyτ، xzτ، yzτ تعریف میشود.
چگونگی ترسیم منحنی تنش–کرنش
دادههای اساسی در مورد خواص مکانیکی یک فلز انعطافپذیر از یک آزمایش کشش بهدست میآید که در آن یک نمونه با طراحی مناسب تحت بار محوری فزایندهای قرار میگیرد تا زمانیکه شکسته شود. بار و ازدیاد طول در طول آزمایش در فواصل زمانی مکرر اندازهگیری و طبق معادلاتی قبلی بهصورت تنش و کرنش متوسط بیان میشوند. دادههای بهدستآمده از آزمون کشش عموما بهصورت نمودار تنش-کرنش رسم میشوند. شکل 4 منحنی تنش-کرنش معمولی را برای فلزی مانند آلومینیوم یا مس نشان میدهد.
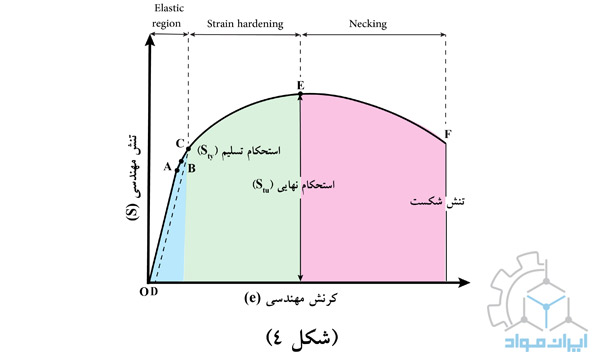
تفسیر منحنی تنش-کرنش:
بخش خطی اولیه منحنی OA ناحیه الاستیکی است که در آن قانون هوک (Hook’s law) رعایت میشود. نقطه B حد الاستیک (Elastic limit) است که بهعنوان بزرگترین تنشی که فلز میتواند بدون تجربه کرنش دائمی هنگام برداشتن بار تحمل کند، تعریف میشود. تعیین حد الاستیک کاملا خستهکننده است و به حساسیت ابزار اندازهگیری کرنش بستگی دارد. به این دلایل اغلب با حد تناسب (Proportional limit) در نقطه A جایگزین میشود. حد تناسب تنشی است که در آن منحنی تنش-کرنش از خطیبودن منحرف میشود. شیب نمودار در منطقه الاستیکی، مدول الاستیسیته (modulus of elasticity) یا مدول یانگ (Young’s modulus) نامیده میشود.
مدول یانگ (Young Modulus) چیست؟
مدول یانگ از چه زمانی مطرح شد؟ مفهوم اساسی مدول یانگ توسط دانشمند و مهندس سوئیسی...همچنین در این ناحیه قانون الاستیسیته خطی یا قانون هوک (معادله6) برقرار است.
معادله 6 (قانون هوک) | S = Ee |
بااینحال، لزوما بهاینمعنی نیست که همهی موادی که رفتار کشسانی دارند، معادله تنش-کرنش خطی دارند. لاستیک (Rubber) نمونهای از یک ماده با معادله تنش-کرنش غیرخطی است که هنوز تعریف یک ماده الاستیک را برآورده میکند.

معرفی چندین نقطه مهم در منحنی تنش-کرنش
A) این حد تناسب است که نشاندهندهی حداکثر مقدار تنشی است که در آن منحنی تنش-کرنش خطی است.
B) این حد الاستیک است که نشاندهندهی حداکثر مقدار تنش است که در آن هیچ تغییر دائمی وجود ندارد. حتی اگر منحنی بین حد تناسب و حد الاستیک خطی نباشد، ماده همچنان در این ناحیه الاستیک است و اگر بار در این نقطه یا کمتر از آن برداشته شود، نمونه به طول اولیه خود باز میگردد.
C) این نقطه تسلیم است که نشاندهنده مقدار تنشی است که در بالای آن کرنش بهسرعت شروع به افزایش میکند. تنش در نقطه تسلیم، استحکام تسلیم، Sty نامیده میشود. این استحکام، تنشی است که در آن مقدار کمی تغییر شکل پلاستیک معمولا به اندازه 2/0 درصد یا 002/0 بهوجود میآید و به نام استحکام تسلیم افست (Offset stress) معروف است. برای مواد بدون نقطه تسلیم کاملا مشخص، معمولا با استفاده از روش افست، 2/0 درصد یا 002/0 تعریف میشود که در آن خطی موازی با بخش خطی منحنی ترسیم میشود که محور x را با مقدار کرنش 002/0 قطع میکند. نقطهای (D) که منحنی تنش-کرنش را قطع میکند بهعنوان نقطه تسلیم تعیین میشود.
E) این نقطه مربوط به استحکام نهایی (Ultimate Tensile strength) یا Stu است که حداکثر مقدار تنش در نمودار تنش-کرنش است. به استحکام نهایی، مقاومت کششی نیز گفته میشود. همانطورکه مشاهده میشود با انجام تغییرشکل پلاستیک پس از نقطه C، ماده دچار کرنشسختی یا کارسختی میشود و درنتیجه استحکام آن افزایش مییابد. در ناحیه CE، تغییر شکل پلاستیک یکنواخت است و در تمامی طول نمونه اتفاق میافتد و سطح مقطع لحظهبهلحظه کوچکتر میشود ولی چون تاثیر کرنشسختی بیشتر است استحکام بالاتر میرود. پس از رسیدن به تنش نهایی، در مواد نرم، گلویی شدن (Necking) رخ میدهد که در آن سطح مقطع در یک ناحیه از نمونه بهطور قابلتوجهی کاهش مییابد.
F) همانطورکه در قسمت قبل بیان شد، در نقطه E که استحکام نهایی نامیده میشود، بیشترین استحکام وجود دارد. از آن به بعد استحکام تسلیم دیگر یکنواخت نیست و در مناطقی از نمونه تغییر شکل و کاهش سطح مقطع نیز مشاهده میشود. طوریکه تاثیر این کاهش سطح مقطع از تاثیر کرنشسختی بیشتر میگردد و در نتیجه استحکام کاهش مییابد. این سیر نزولی ادامه مییابد تا اینکه نمونه در نقطه F میشکند. به استحکام در نقطه F، استحکام شکست (Fracture Strength) میگویند.
پیشنهاد میکنیم:
مدول یانگ (Young Modulus) چیست؟
مدول یانگ از چه زمانی مطرح شد؟ مفهوم اساسی مدول یانگ توسط دانشمند و مهندس سوئیسی...مدول الاستیسیته
لازمبهذکر است که مدول الاستیسیته (E)، معیاری برای سفتی (Stiffness) ماده است که همان مقاومت در برابر تغییر شکل است. هرچه این مدول بیشتر باشد کرنش الاستیکی در یک تنش ثابت کمتر است. مدول الاستیسیته یکی از پارامترهای مهم در طراحی است؛ زیرا برای محاسبه میزان تغییرشکل الاستیک مواد مشخصشدن این پارامتر ضروری است. مدول الاستیسیته ناشی از نیروهای پیوستگی بین اتمهای ماده است و این نیروها نیز بدون تغییر بنیادی ماده، تغییر زیادی نمیکنند. این مدول همانند نقطهذوب وابسته به انرژی پیوند بین اتمهای ماده است و با هم رابطه مستقیمی دارند. بهطوریکه مواد با نقطهذوب بالا دارای مدول یانگ بالاتری هم هستند. اما افزایش دما موجب کاهش شدید آن میشود؛ زیرا نیروهای پیوستگی بین اتمهای ماده کاهش مییابد.

مدول الاستیسیته وابسته به ساختار کریستالوگرافی آنها نیست. درو اقع تفاوت چندانی بین مدول الاستیسیته آهن با ساختار bcc و آهن با ساختار fcc مشاهده نمیشود. همچنین، عملیات حرارتی که با تغییر ساختار میتواند سختی و استحکام آلیاژها را تغییر دهد تاثیرچندانی روی این مدول نمیگذارد. حتی کار سرد و اضافهکردن مقدار کم عناصر آلیاژی نیز روی مدول الاستیسیته تاثیر کمی میگذارد. زیرا پیوندهای کمی تحت تاثیر این عملیات قرار میگیرند. اما افزودن مقدار زیادی از یک عنصر، بهخصوص با نقطه ذوب بالاتر، میتواند مدول الاستیسیته آلیاژ را بالا ببرد.
نسبت پوآیسون (Poisson’s ratio)
در اثر اعمال نیروی کشش و ایجاد کرنش کششی در جهت x، در جهتهای y و z نیز انقباض بهوجود میآید. بهتجربه مشخص شده است که کرنش عرضی جزء ثابتی از کرنش طولی است. این مقدار ثابت نسبت پوآیسون (Poisson’s ratio) نامیده میشود و با حرف ѵ مشخص میگردد. بنابراین:
معادله7 | εz = εy = −ѵεx = |
نسبت پوآیسون برای یک ماده کاملا همسانگرد الاستیک برابر با 25/0 است ولی برای اغلب فلزات حدود 33/0 است.
تنشهای برشی اعمالی نیز باعث ایجاد کرنشهای برشی میشود.
معادلات 8، 9 و 10 | τ = Gγyz | τ = Gγyz | = Gγxy τ |
در معادلات بالا، G مدول الاستیسیته برشی یا مدول صلبیت (Shear elasic or rigid modulus) نامیده میشود. مقدار G از آزمایش پیچش تعیین میگردد.
آیا مواد در مقابل کشش، شکست یکسانی را تجربه میکنند؟
رفتار کلی مواد تحتبار را میتوان بسته به اینکه آیا ماده توانایی تغییر شکل پلاستیک را نشان میدهد یا نه، بهعنوان نرم یا انعطافپذیر (ductile) و ترد یا شکننده (brittle) طبقهبندی کرد. در شکل4، منحنی تنش-کرنش کششی یک ماده انعطافپذیر، نشان داده شده است. شکل5، دو رفتار متفاوت را در مواد ترد مقایسه میکند. شکل5-الف، رفتار یک ماده کاملا شکننده که تقریبا در حد الاستیک شکسته میشود را نمایش میدهد، درحالیکه شکل 5-ب، یک فلز شکننده، مانند چدن سفید را نشان میدهد که مقداری انعطافپذیری جزئی را قبل از شکست تحمل میکند.
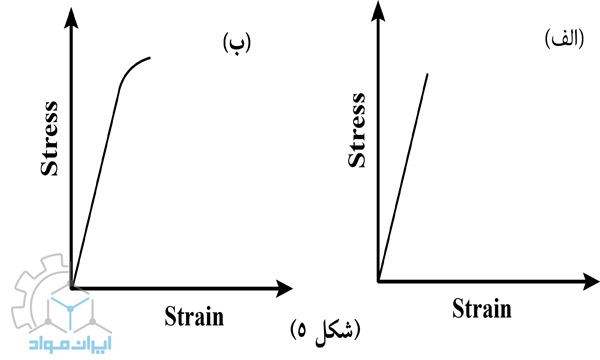
ب: رفتار یک فلز شکننده با انعطاف پذیری جزئی پیش از شکست.
داشتن توانایی شکلپذیری کافی برای مواد یکی از ملاحظات مهندسی مهم است، زیرا به مواد اجازه میدهد تنشهای موضعی را در ماده توزیع کند. از طرفی تغییر شکل پلاستیک باعث کور شدن ترک و جلوگیری از پیشروی ترک میشود. در مواد ترد، حتی اگر هیچ غلظت تنشی در یک ماده شکننده وجود نداشته باشد، شکست همچنان بهطور ناگهانی رخ میدهد زیرا تنش تسلیم و استحکام کششی عملا یکسان هستند. توجه به این نکته ضروری است که شکنندگی خاصیت مطلق یک فلز نیست. فلزی مانند تنگستن که در دمای اتاق شکننده است، در دمای بالا انعطافپذیر است. فلزی که در کشش شکننده است ممکن است تحت فشار هیدرواستاتیکی انعطافپذیر باشد. علاوهبراین، فلزی که در دمای اتاق از نظر کشش انعطافپذیر است، میتواند در حضور ترکها، دمای پایین، سرعت بالای بارگذاری، یا عوامل شکننده مانند هیدروژن ترد شود.
شکست در نمونههای نرم یا با گلویی شدن (Necking) و باریک شدن نمونه تا یک نقطه، یا با مخروطی و فنجانی شدن (Cup and cone)، یا با برش (Shear) نمونه اتفاق میافتد.
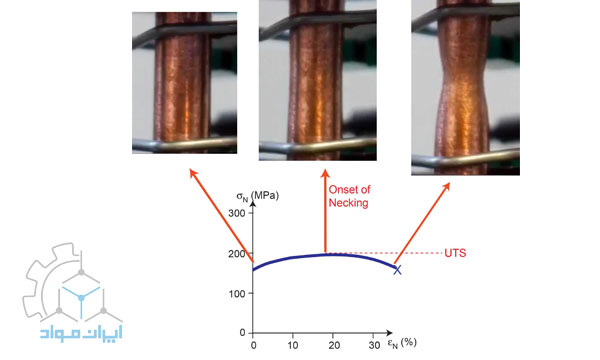
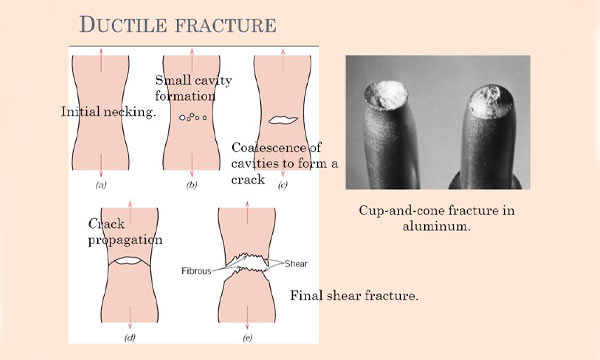
منحنی تنش-کرنش حقیقی (True-stress True Strain curve)
منحنی تنش-کرنش مهندسی، نشاندهندهی واقعی مشخصات تغییر شکل فلزات نیست زیرا کاملا براساس ابعاد اولیه نمونه است و این ابعاد مرتبا در طی آزمایش در حال تغییر هستند. شکل6 یک منحنی تنش-کرنش مهندسی را در مقایسه با منحنی تنش-کرنش واقعی نشان میدهد. همانطورکه مشاهده میشود در منحنی تنش-کرنش مهندسی، پس از عبور از نقطهی استحکام نهایی، چون سطح مقطع شدیدا کاهش مییابد. بنابراین نیروی لازم جهت تغییر شکل نیز کاهش پیدا میکند و چون این نیرو تقسیم بر سطح مقطع اولیه نمونه میگردد، بنابراین پس از عبور از نقطه ماکزیمم، افت شدید تنش بهوجود میآید. اما در منحنی تنش-کرنش حقیقی، همواره تنش در اثر کرنش سختی سیر صعودی دارد تا اینکه نمونه دچار شکست شود و بهعبارتی تنش واقعی بیشتر از تنش مهندسی است.
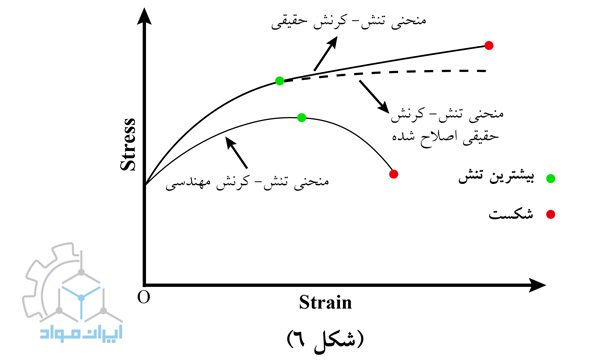
یکی از پارامترهایی که از منحنی تنش-کرنش حقیقی بهدست میآید تنش حقیقی در حداکثر بار است. این تنش با σu نشان داده میشود و به استحکام کششی حقیقی گزارش شده است. σu وقتی اتفاق میافتد که سطح مقطع Au و مقدار کرنش εu است. در حداکثر بار استحکام نهایی کششی یا Su اتفاق میافتد.
انرژی تنش (Strain Energy)
هنگامیکه نیرو به یک ماده وارد میشود، ماده تغییر شکل میدهد و مانند فنر انرژی پتانسیل را ذخیره میکند. انرژی کرنش (یعنی مقدار انرژی پتانسیل ذخیره شده در اثر تغییر شکل) برابر با کاری است که برای تغییر شکل ماده صرف میشود. انرژی کرنش کل مربوط به مساحت زیر منحنی نیرو-جابهجایی (Load- deflection curve) است و دارای واحدهای in-lbf در سیستم معمول ایالات متحده و N-m در سیستم SI است. انرژی کرنش الاستیک را میتوان بازیابی کرد، بنابراین اگر تغییر شکل در محدوده الاستیک باقی بماند، آنگاه میتوان تمام انرژی کرنش را بازیابی کرد.
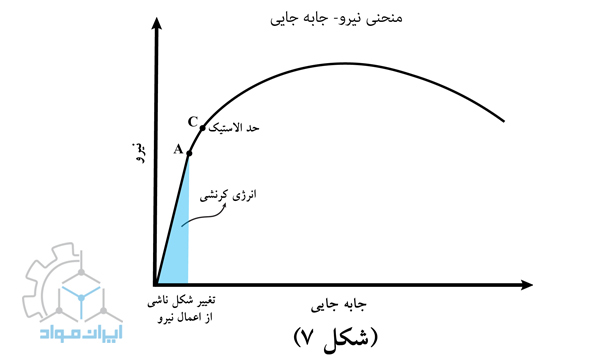
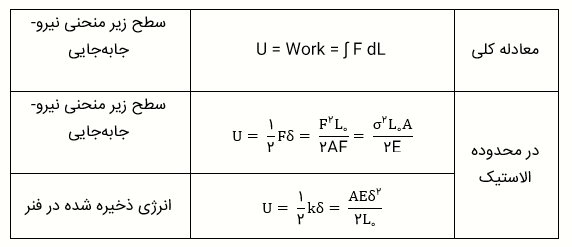
توجه داشته باشید که دو معادله برای انرژی کرنش در محدوده الاستیک وجود دارد. معادله اول براساس مساحت زیر منحنی نیرو-جابهجایی است. معادله دوم براساس معادله انرژی پتانسیل ذخیره شده در فنر است. هر دو معادله نتیجه یکسانی را به دست میدهند، فقط تا حدودی متفاوت استخراج شدهاند.
نتیجه گیری:
منحنی تنش-کرنش بسیاری از پارامترهای مهم و مورد نیاز برای طراحی قطعه یا مواد را در اختیار مهندسان طراح قرار میدهد. نمودار تنش-کرنش خواص مکانیکی زیادی مانند استحکام، چقرمگی، الاستیسیته، نقطه تسلیم، انرژی کرنش، انعطافپذیری و ازدیاد طول در طول بار را در اختیار ما قرار داده است و در نظر گرفتن تمامی این موارد مهندسین را در ساخت قطعات و مواد باکیفیت بالاتر راهنمایی میکند. بنابراین دانستن مفهوم تنش و کرنش و تفسیر نمودارهای آنها برای هر مهندسی به ویژه مهندسین مواد و متالورژی امری بسیار ضروری و حیاتی است. چه به دنبال انجام اکستروژن، نورد و خمش باشید و یا هر عملیات دیگری؛ امیدواریم نکات ذکر شده در این مقاله برای شما مفید واقع شده باشد.
منابع:
Dieter, G. E., & Bacon, D. (1976). Mechanical metallurgy (Vol. 3, pp. 43-53). New York: McGraw-hill.
سید عبدالکریم سجادی،” رفتار مکانیکی مواد”، مشهد، انتشارات دانشگاه فردوسی مشهد، ویرایش دوم،1384.
https://mechanicalc.com/reference/mechanical-properties-of-materials











دیدگاه کاربران
بسیار عالی بود
خیلی خوب توضیح دادی مرسی از سایت خوبتون
عالی و کامل