خزش و مکانیزم های آن (Creep and Mechanisms)

خزش و مکانیزم های آن

تئوری خزش

خزش، تغییر شکل مومسان (Plasticity) وابسته به زمان مواد، در دماهایی بالاتر از نصف نقطه ذوب و در محدوده تنش هایی زیر حد الاستیک ماده، می باشد. در عمل خواص کششی اغلب فلزات در دمای اتاق، تقریبا مستقل از زمان می باشد اما در دمای بالا، وابستگی استحکام به سرعت بارگذاری و زمان، مشاهده می شود و ماده ای که تحت بارگذاری کششی در دمای بالا قرار دارد، دچار خزش می شود.

دمایی که در آن خزش اتفاق می افتد به جنس ماده وابسته است، به گونه ای که دمایی که برای یک ماده بالاست، ممکن است برای ماده دیگر بالا نباشد تا خزشی صورت گیرد. این دما در مجموع به نقطه ذوب ماده بستگی دارد. معمولا خزش در دماهای بالاتر از نصف نقطه ذوب رخ می دهد.

شکل ۱ منحنی خزش را تحت شرایط تنش ثابت نشان می دهد. سه ناحیه در این منحنی مشخص شده است:

• ناحیه اول خزش اولیه (Primary): ناحیه ای است که با گذشت زمان نرخ کرنش خزشی کاهش می یابد.
• ناحیه دوم خزش ثانویه یا خزش پایا (Steadystate): ناحیه ای که در آن نرخ خزش ثابت است و نتیجه تعادل بین فرایندهای کارسختی (Workhardening) و بازیابی (Recovery)، برقرار است.
• ناحیه سوم خزشی (Tertiary creep): با تشکیل حفره ها، ترک و ناپایداری ریزساختاری، نرخ کرنش افزایش یافته و نهایتا به شکست نمونه منجر می گردد. برخی اوقات مرحله یک مستقیما به مرحله سه منجر شده و نوعی خمیدگی در آن مشاهده می شود.

نمودار رفتار خزشی در حالت تنش ثابت.

در شکل ۲ نیز تغییر شکل مومسان تحت شرایط کرنش ثابت مشاهده می شود. در ناحیه I تحت شرایط نرخ کرنش ثابت، فلز سخت می شود و لذا به افزایش تنش سیلان می انجامد. اغلب در فلزات خالص، تنش و نرخ کرنش به ترتیب، تا مقداری که در گستره ای از کرنش ثابت است، افزایش و کاهش می یابند (مرحله II) که این مرحله همان خزش ثانویه یا حالت پایا است. در مرحله III، تشکیل حفرات، ترکها و ناپایداری های ریز ساختاری، منجر به افزایش نرخ کرنش ظاهری و نهایتا شکست نمونه می شوند.

نمودار رفتار خزشی در حالت کرنش ثابت.

مکانیزم های خزش (Creep Mechanisms)

1. خزش ناشی از نفوذ (Diffusion creep)

تنش خارجی می تواند حرکت و نفوذ جای خالی اتمی (Vacancy) را از طریق شبکه‌ی بلوری یا از طریق مرزدانه کنترل کند و باعث تغییرشکل مومسان شود. بنابراین، دو نوع خزش نفوذی وجود دارد:

• خزش نفوذی از طریق دانه ها یا خزش نابارو-هرینگ (Nabarro-Herring)
• خزش نفوذی از طریق مرزدانه ها یا خزش کوبل (Coble)

در خزش کششی بر اثر نفوذ جای خالی اتمی و حرکت هم زمان اتم ها در جهت مخالف، دانه ها در امتداد تنش به طولشان افزوده می شود و در امتداد عمود بر تنش از طولشان کاسته می شود. در خزش نفوذی مرزدانه ای یا خزش کوبل، مهاجرت جاهای خالی اتمی از مرزدانه های تحت کشش به مرزدانه های تحت فشار از طریق مرزدانه ها انجام می شود.

2. لغزش مرزدانه ای  (Grain- boundary sliding)

لغزش مرزدانه ای یک فرآیند برشی است که در امتداد مرزدانه ها اتفاق می افتد و با افزایش دما و کاهش نرخ کرنش افزایش می یابد. در دماهای بالا، دانه های فلزات پر بلور (Poly crystal) می توانند نسبت به یکدیگر حرکت کنند. لغزش مرزدانه ای اغلب در اثر فعالیت هم زمان مکانیزم هایی مانند کوبل و نابارو-هرینگ اتفاق می افتد و در طی این اتفاق شکل دانه حفظ می شود. از ویژگی های لغزش مرزدانه ای این است که هم به خزش نفوذی و هم به خزش نابجایی (Dislocation creep) مربوط می شود.

3. خزش نابجایی (Dislocation creep)

خزش نابجایی، ایجاد تغییر شکل خزشی توسط نابجایی در اثر نفوذ جای خالی اتمی و یا برش است. خزش نابجایی را خزش قانون توانی (Power law creep) نیز می گویند. یکی از مکانیزم های خزش نابجایی، صعود نابجایی است (Dislocation climb) که با نفوذ جای خالی انجام می شود. در دمای بالا، اگر یک نابجایی لبه ای (Edge dislocation) متحرک، به وسیله‌ی یک مانع متوقف شود، صعود نابجایی می تواند باعث عبور آن از مانع با تغییر صفحه لغزش شود. مکانیزم لغزش نابجایی تقریبا همه‌ی کرنش را باعث می شود، اما صعود نابجایی سرعت تغییرات کرنش را کنترل می کند.

مکانیزم دیگر در عبور از موانع، لغزش متقاطع (Cross slip) نابجایی پیچی (Screw dislocation) است.

نوع دیگر خزش نابجایی، برش است که توسط مکانیزم نقص چیدمان (Stacking fault) انجام می شود. وقتی یک نابجایی به یک رسوب می رسد می تواند آن را ببرد و از آن عبور کند. این نابجایی خود به دو نابجایی ناقص (Partial dislocation) تجریه می شود و چون با تجزیه شدن مقدار کل انرژی نابجایی کاهش می یابد، بنابراین این کار به سهولت انجام می شود.

4. خزش لغزش چسبنده  (Viscous glide creep)

در خزش لغزش چسبنده، مکانیزم تغییر شکل لغزش چسبنده نابجایی ها است. نابجایی ها به چند طریق با اتم های حل شونده (Solute) برهم کنش دارند و همین امر از حرکت آنها جلوگیری می کند. در گستره تنشی این رفتار، دو مکانیزم رقابتی وجود دارند: صعود و لغزش نابجایی.

از آنجا که لغزش نابجایی آهسته تر صورت می گیرد، بنابراین کنترل کننده سرعت است. رابطه‌ی ۱، معادله خزش لغزش چسبنده را نشان می دهد :

در این رابطه، A یک پارامتر برهم کنش است که نوع فرآیند کشش چسبنده لغزش نابجایی را مشخص می کند. مطالعات نشان می دهند که چند فرآیند محتمل برای کشش چسبنده توسط اتم محلول وجود دارند:

فرآیند کشیدن (Dragging) می تواند به علت جدایش اتمسفر اتم حل شونده به سمت نابجایی های متحرک باشد که سرعت نابجایی توسط نرخ مهاجرت اتم های حل شونده محدود می شود. همچنین در آلیاژهای محلول جامد با نظم کوتاه برد (Short-range-ordered alloys)، حرکت نابجایی ها نظم را برهم می زند و یک فصل مشترک ایجاد می کند و از آنجا که منظم شدن موضعی ناشی از تنش اتم های حل شونده، مانع حرکت نابجایی است، لذا منظم شدن ناحیه اطراف یک نابجایی انرژی بلور را کاهش می دهد.

حرکت یک نابجایی در آلیاژهای با نظم بلند برد (Long-rang-ordered alloys) نیز محدود است، زیرا گسترش مرز ضد فازی (Anti-phase boundary)، منجر به افزایش انرژی می گردد. بنابراین ثابت A در معادله ۱ مجموع برهم کنش های متفاوت احتمالی نابجایی ها با اتم های حل شونده است.

5. شکست قانون توانی (Power-law Breakdown)

در تنش های پایین، رابطه توانی بین نرخ کرنش و تنش مشاهده می شود ولی خزش در تنش های بالا اغلب منجر به کرنش هایی می شود که از رابطه قانون توانی پیروی نمی کنند. در تنش های بالا، نرخ های کرنشی که مشاهده می شوند به مراتب از آنچه قانون توانی پیش بینی می کند، بالاتر هستند. این پدیده به عنوان شکست قانون توانی عنوان شده است.

مطالعات مرتبط با مکانیزم خزش در تنش های بالا، برای شکست قانون توانی دو عامل پیشنهاد می کنند: نقض قانون توانی یک مکانیزم تغییر شکل ذاتی است یا این که مکانیزم خزش به علت افزایش تنش تغییر می کند. بارت و نیکس و ورتمن نظریه هایی را بیان کردند که نقض قانون توانی یک مکانیزم تغییرشکل ذاتی است و رابطه بین تنش و نرخ کرنش شامل یک عبارت سینوس هایپربولیک است.

مدل بارت و نیکس، معادلات نرخ کرنش حالت پایا را بر مبنای حرکت کنترل شده با نفوذ نابجایی های پیچی جاگ دار بیان می کند. فرض شده است که جاگ ها، یک نیروی کششی ایجاد می کنند که منجر به ایجاد یک رابطه سینوس هایپربولیک بین نرخ کرنش و تنش می شود.

مدل ورتمن، خزش نابجایی کنترل شده با صعود را مفروض دانسته که حالت پایا به واسطه صعود و از بین رفتن نابجایی ها حاصل می شود. مطالعاتی که شکست قانون توانی را یک تغییر در مکانیزم تغییرشکل می داند، مشخص کرده اند که در تنش های کمتر، رفتار قانون توانی مشاهده می شود. در این خصوص، مکانیزم پذیرفته شده صعود نابجایی کنترل شده با نفوذ است که نابجایی برای عبور از موانع صعود می کند یا توسط نابجایی با علامت مخالف حذف می شود. در تنش های بالا که رفتار نمایی مشاهده می شود، چندین مکانیزم شامل این موارد پذیرفته شده است:

• انتقال از صعود به لغزش
• اندرکنش شیمیایی جاگ ها با جاهای خالی فوق اشباع
• حرکت جاگ ها و مهاجرت جاگ
• صعود نابجایی های لبه ای

آزمون خزش مواد 

نتایج آزمون خزش در طراحی اجزای صنعتی و ساختمانی که در دمای بالا کار می کنند اهمیت بالایی دارند. به عنوان مثال مخازن نفتی موجود در پالایشگاه بایستی به گونه ای طراحی شوند که استحکام مناسب را در برابر تنش اعمالی از طرف سیال در دمای بالا و در مدت طولانی داشته باشند.

[read_this]

درست است که خزش در هر دمایی رخ می دهد اما اهمیت خزش به ماهیت ماده، دمای کاری و مقدار تغییر شکل مجاز قطعه بستگی دارد. تست خزش فرآیندی بسیار طولانی است و آزمایشگاه تست خزش نیاز به تعداد بسیار زیادی تجهیزات دارد. حتی شاید حدود صدها دستگاه آزمون خزش در یک آزمایشگاه لازم باشد؛ بنابراین آزمون خزش بسیار پر هزینه است. مشخصا آزمون خزش همان آزمون کشش است که در تنش و دمای ثابت انجام می شود. در این آزمون از یک وسیله بسیار دقیق اندازه گیری طول (معمولا کرنش سنج) و یک وسیله گرم کردن نمونه در شرایط کاملا کنترل شده استفاده می شود.

دستگاه تست خزش

روش متداول برای آزمون خزش مواد، استفاده از یک کوره مقاومتی استوانه ‌ای است که روی قاب ماشین کشش نصب می ‌شود و در جهت قائم قابل جابه‌جایی است. کوره می ‌تواند در امتداد هادی خود به طرف بالا و پایین حرکت کند تا در مکانی مناسب، نمونه را دربر گیرد یا اینکه به فاصله مناسبی از آن قرار گیرد به ‌طوری که گذاشتن و برداشتن نمونه آزمایش و همچنین تنظیم سیستم کرنش سنج امکان ‌پذیر باشد.

کوره باید به مقدار قابل ملاحظه ‌ای از طول نمونه آزمایش بلندتر باشد تا اطمینان از برقراری دمای یکنواخت در تمام طول نمونه حاصل شود. کوره‌ هایی که برای آزمایش خزش مورد استفاده قرار می‌ گیرند معمولا دارای چند ناحیه هستند که هر یک از آن‌ ها می ‌تواند مستقلا کنترل شود. به این ترتیب افت‌ دما، که معمولا در دو انتهای استوانه کوره وجود دارد، جبران می ‌شود.

در طول‌ گیج نمونه باید چندین ترموکوپل دقیق قرار داده شود. حساسیت وسایل اندازه‌گیری دما باید به ‌قدری باشد که حتی تغییرات نیم درجه سانتیگراد یا کمتر از آن را نیز اندازه‌گیری کنند.

بیشتر کرنش‌ سنج‌ هایی که برای تست خزش به‌ کار گرفته می‌ شوند، دارای امکانات انتخاب مبدا اندازه‌گیری نیز هستند. لذا می‌ توان برد اندازه‌گیری آن‌ ها را تغییر داد و قرائت دقیق‌ تری برای افزایش طول‌ های بزرگ‌ تر به‌ دست آورد. اگر انتهای بازو های کرنش‌ سنج‌ ها به طرفین نمونه آزمایش متصل شود، ممکن است در قرائت طول مشکلاتی ایجاد شود. در مقابل می‌ توان بازو های کرنش‌ سنج را در محدوده‌ ای خارج از قسمت اندازه‌ گیری با استفاده از تیغه‌ های تماس لبه تیز به گیج متصل نمود.

•  قراردادن نمونه در دستگاه  

اتصالات نمونه و دستگاه در تست خزش باید بسیار استوار باشند تا در طول آزمایش، محل آن‌ ها تغییر نکند. به‌ ویژه اگر لازم باشد آزمون در دماهای خیلی بالا انجام شود. به هر حال، زیاد محکم کردن گیره ‌های لبه تیز دستگاه، روی نمونه می ‌تواند فرورفتگی‌ هایی ایجاد کند که نهایتا رفتار خزشی نمونه تحت آزمایش را دچار تغییر کند.

در روش دیگر اتصال، کرنش‌ سنج‌ ها به شانه‌ هایی که خارج از قسمت اندازه‌گیری نمونه قرار دارند متصل می‌ شوند. از آنجا که سطح مقطع نمونه آزمایش از قسمت میانی تا نقاط اتصال روی شانه‌ ها در یک فاصله کوتاه به مقدار زیادی تغییرات دارد، مقدار افزایش طولی که  روی شانه ‌ها ایجاد می‌شود ناچیز است. اگر نقاط اتصال نزدیک لبه های نمونه باشند، در این صورت افزایش طول اندازه‌گیری شده در اثر خزش، نمایش تقریبا دقیقی از افزایش طول متناظر با طول قسمت گیج نمونه خواهد بود.

•  قوانین تلورانس دمایی در تست خزش

در آزمون خزش استاندارد، ابتدا نمونه همراه با ترموکوپل و کرنش‌ سنج متصل به آن تا دمای انجام آزمایش گرم می‌شود و سپس بارگذاری انجام می‌ شود. باید توجه داشت که نیرو به تدریج افزایش یابد و ازدیاد طول ناشی از افزایش بار تا رسیدن به تنش اسمی باید ثبت شود.

تلورانس دمایی در تست خزش اهمیت زیادی دارد که در استانداردها ذکر شده است. طبق استاندارد، برای انجام آزمایش تا ۶۰۰ درجه سانتی گراد، باید دماها تا حدود ۲± درجه سانتی گراد ثابت باشند. برای محدوده ۶۰۰ تا ۸۰۰ درجه سانتی گراد، این مقدار ۲٫۵± درجه سانتی گراد بوده و در دماهای بین ۸۰۰ تا ۱۰۰۰ این مقدار ۳± درجه سانتی گراد تبیین گردیده است. برای رسیدن به این شرایط، نه تنها باید کوره به دقت ساخته شود و توسط ترموکوپل کنترل شود بلکه باید وسایل اندازه‌گیری دما از دقت و حساسیت بالایی برخوردار باشند.

 نتایج آزمون خزش

پیش بینی رفتار خزشی به دلیل تشخیص استحکام مواد در دمای بالا از جمله مواردیست که استفاده وسیعی در طراحی بسیاری از سازه های مورد کاربرد در دمای بالا دارد. روش معمول برای این پیش بینی، برون یابی داده های گسیختگی ناشی از خزش است. طبیعتا این برون یابی ها با بکارگیری نتایج حاصل از تست خزش صورت می گیرند و نمودارهای مربوط به هر مدل رسم می گردند. مهم ترین پارامترها (مدل ها)یی که در طراحی مواد در دمای بالا کاربرد دارند، در جدول زیر گردآوری شده اند.

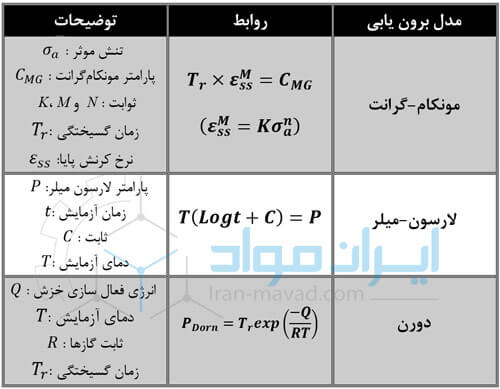
نتایج آزمون خزش دارای پراکندگی هستند و نمی توان که برای یک دما و تنش به خصوص، فقط به نتایج یک آزمون اکتفا کرد. برای به‌ دست آوردن تصویر کاملی از مشخصات خزشی ماده، به‌ ازای هر ترکیبی از تنش و دما، انجام چندین آزمون و ثبت نتایج آن لازم است. با وجود این، حتی اگر هر ترکیبی از ویژگی‌ های خزشی ماده در دوره‌ های نسبتا کوتاه ۱۰۰۰ یا ۱۰۰۰۰ ساعته در دسترس باشد، بسیار مشکل است که عملکرد خزشی آن ماده را در یک دوره طولانی از عمر ضمن خدمت، پیش‌ بینی کرد.

با وجود این مسئله، نتایج آزمایش خزش را می‌ توان با اطمینان کافی برای مقاصد طراحی مورد استفاده قرار داد. مشروط بر این که شرایط کار، شامل مقادیر نسبتا ثابتی از تنش و دما در دوره‌ های طولانی کاری باشد.

فیلم تست خزش مواد

در پایان توجه شما را به مطالعه‌ی سایر تست های مخرب که در همین وب سایت تهیه شده جلب می نماییم:

• آزمون کشش (Tensile test)
• آزمون فشار (Compression Test)
• آشنایی با تست ضربه (Impact Test)
• تست خمش مواد (Bending Test)
• مروری بر روش های سختی سنجی مواد (Haedness Test)
• از خستگی در مواد چه می دانیم؟ (Fatigue Test)
• متالوگرافی و کاربردهای آن (Metallography)

منابع و مراجع

1. س.ع. سجادی،سوپر آلیاژهای پایه نیکل. مشهد : دانشگاه فردوسی، ۱۳۹۲٫
2. کاسنر، ام. ای. (۱۳۹۱)، مبانی خزش فلزات و آلیاژها، ترجمه سید عبدالکریم سجادی، چاپ اول، نشر مشهد.

-D.R. Lesuer, C.K. Syn, O.D. Sherby,” Evaluation of power law breakdown in metals, alloys and dispersion hardened materials and compounds”, Materials Science and Engineering, 2000.

-C.R. Barrett and W.D. Nix, “A model for steady state creep based on the motionof jogged screw dislocations”, Acta Materialia, 13, 1247-1258, 1965.

-J. Weertman, “Steady-state creep through dislocation climb”, J. Applied Physics, 28, 362-364, 1957.